はじめに
こんにちは. 夏休みで暇になったので前々から考えてた記事を形にしようと思います. いつの間にか夏休みが終わってました. どうして… ズレにズレこんでアドカレで公開することになりました. タイミングが…なくて…
多様体とか関手とか難しそうな言葉が並んでますがあんまり気にしないでください. ゆる~くやっていきます. 前提知識はとくにありません.
※この記事では用語とか定義とかを適当に流したり嘘をついたりします. 詳しい方々におかれましてはどうか見逃してください.
用語
さて, そうは言いましたが軽く用語の説明をしておきます. 多様体とは, まあざっくりいうと「図形」のことです. ボールとかドーナツとかをイメージしてみてください. そして関手とは, ちょっと説明が難しいんですが, 「世界を変換するもの」のことです. なんか中二病みたいで恥ずかしいですね. †世界を変換するもの†
世界っていうのはここでは「モノ」がいくつかあって(1つでもいいけど), さらにモノとモノを繋ぐ「矢印」があることを指します. また, 終点と始点が同じ矢印は繋ぐことができます. どういうことかというと, が
から
への矢印で,
が
から
への矢印なら,
から
に
っていう矢印を作ることができるということです.
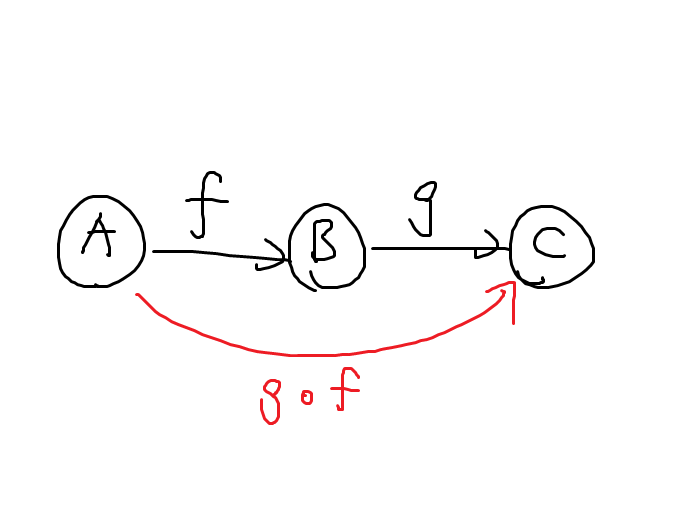
こんな世界を数学の言葉では「圏」って言ったりします.
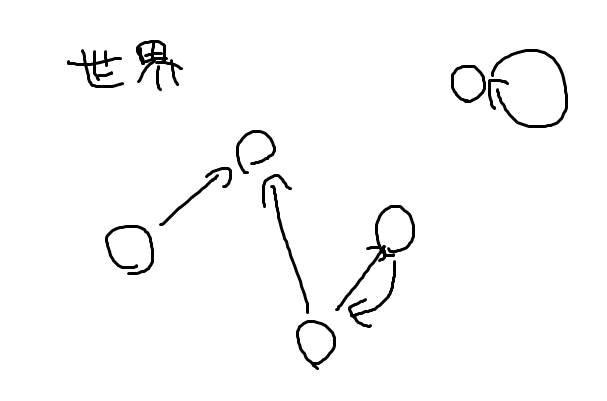
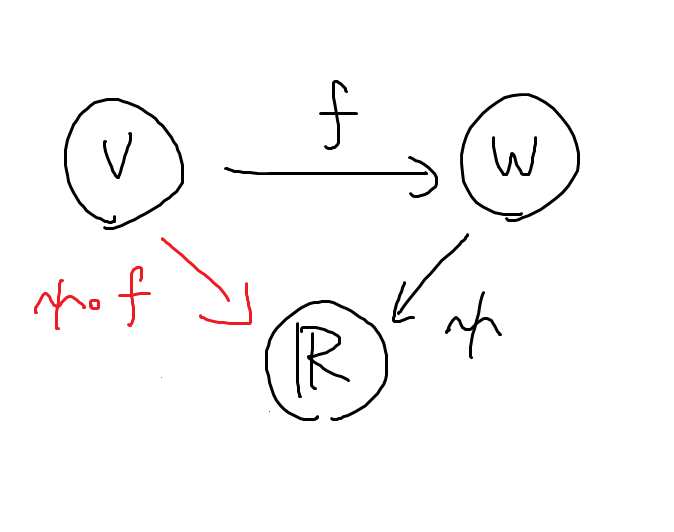
さて本題の関手こと†世界を変換するもの†ですが, これはモノを別の世界のモノに, そしてその間の矢印を対応するモノ間の矢印に変換します. 書いてみましょう.
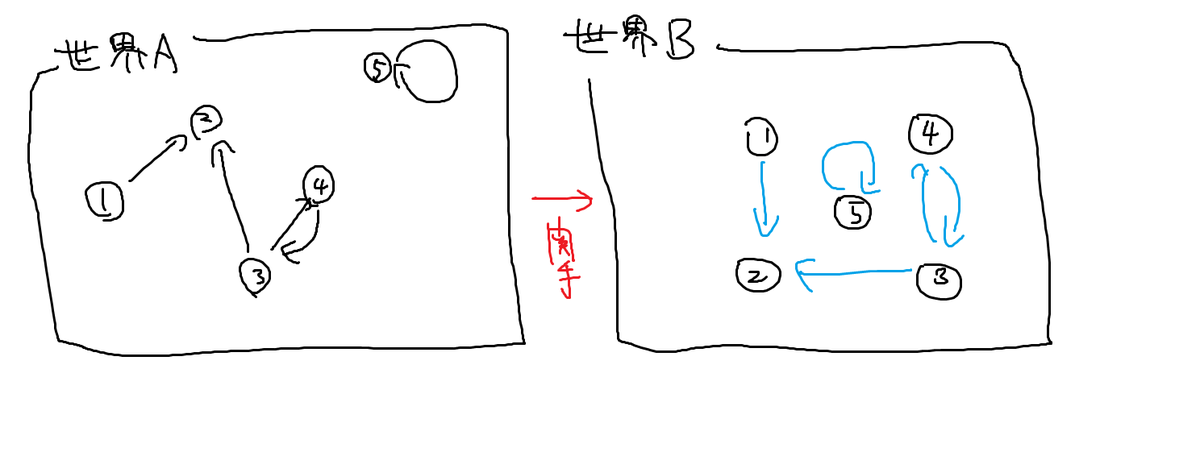
対応するモノに同じ番号を振りました. 矢印の向きは同じにしましたが, 一斉に反対になることもあります.
矢印が関手によって移った先の矢印を
って書いたりします. 向きが反対になる場合は上付きで
です.
本題
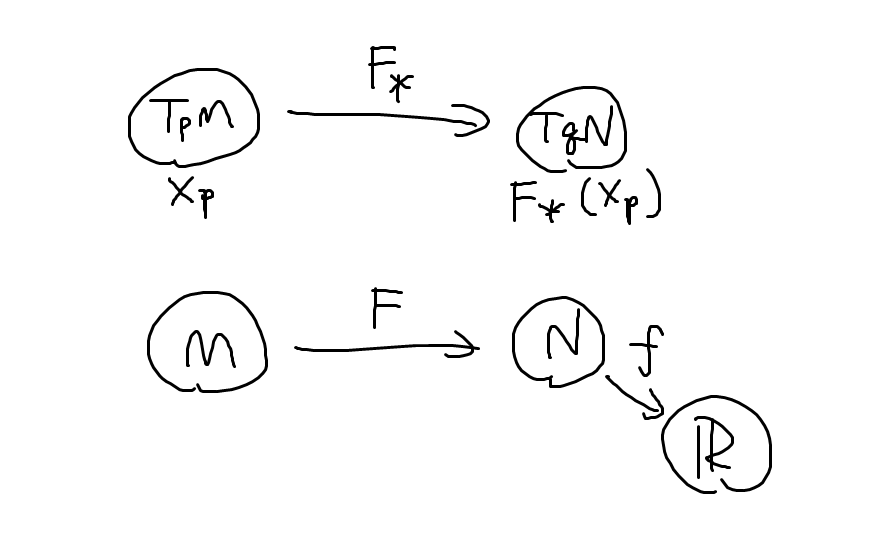
接空間と写像の微分
さて, 本題に入りましょう. モノを多様体, 矢印を(級)写像とする世界を考えます. 多様体
に対して点
を取ると, 接空間
なるものが定義できます. こいつは線型空間になっていて, 多様体がぐにゃぐにゃしているのに対して線形空間はまっすぐなので扱いやすいんですね. イメージ的にはその点で”接している”空間なんですが, ここでは中身に注目するのであんまり気にしないで大丈夫です.
(基点付き)多様体の世界から線形空間の世界への関手を作っていきます. モノ()の行き先は接空間(
)としましょう.
モノの行き先が決まったところで, 矢印の行き先を決めたいんですが, そのためにはの中身を具体的に見ていかないといけません. まぁここもざっくりいきます.
の元(中身の意味)は実は写像で,
から実数
への矢印を受け取って実数を返す”変換器”のようになっています.
を
の元,
を
から
への矢印とすると, 変換先である
が実数になっているということです.
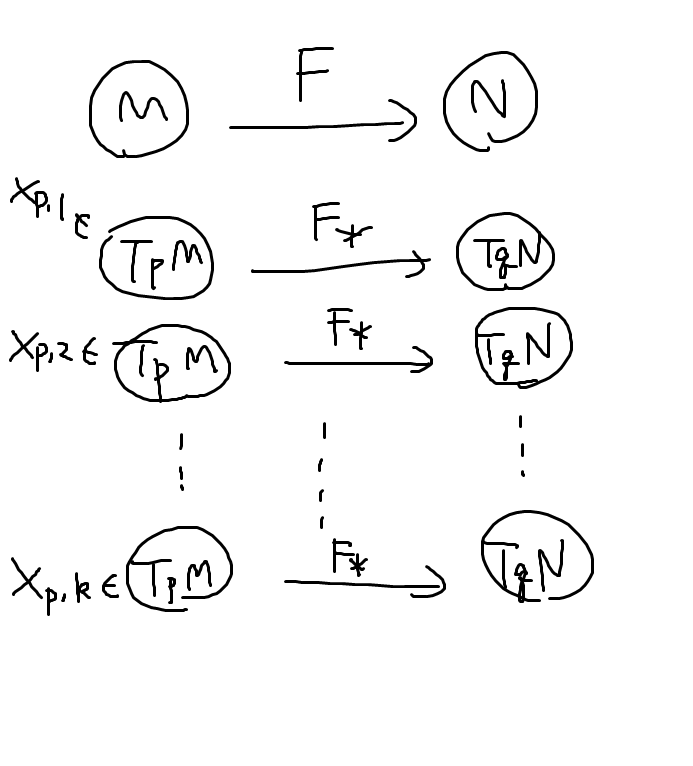
それでは矢印を変換していきましょう. を多様体,
を
から
への矢印,
とします.
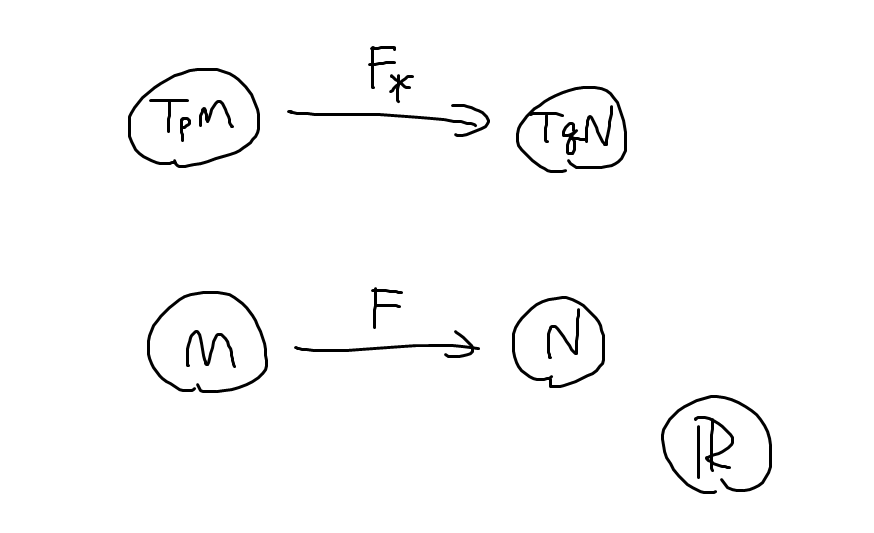
を決めるには
の行き先
を決めればOKです. ここで,
の元は
から
への矢印を受け取って実数を返す写像でした. それではそんな矢印
を食わせてみましょう.
こいつらをつなぎ合わせて実数をゲットしたいわけです. よ~く見てください. は
から
への矢印があれば実数を返せました.
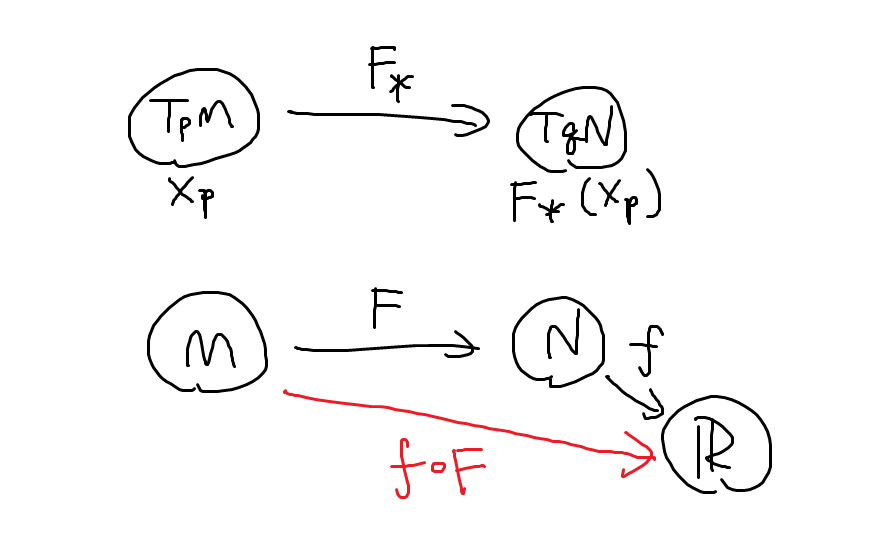
と
を繋ぐことで欲しい矢印が作れました. そんなわけで,
に
を食わせてやって得られた実数をこの
に
を食わせた値としましょう. 式にすると
です. この
を
の微分って呼びます.
どうでしょうか. なんだかとっても”自然”な感じがしませんか?最低限の情報を与えてやれば, そいつらをパズルみたいに組み合わせることで欲しい物が取り出せちゃうんです. 多様体論に限らず, 数学にはこのような”自然さ”があふれています. 高度に抽象化されて意味のわからないことばかりしているイメージのある数学ですが, その根底には”自然な”定義, 発想, 手法が根ざしているんですね.
微分形式の準備:双対空間
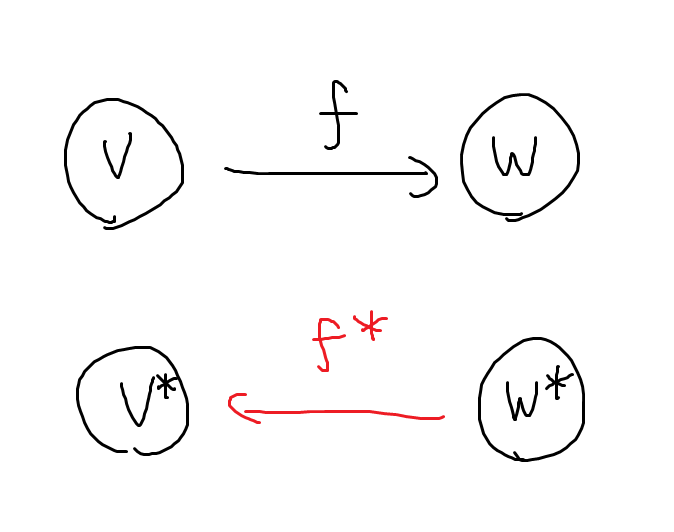
この記事の最終目標ことみんな大好き微分形式の説明をしていきたいんですが, その前に線形空間の双対について説明しておかなければなりません. これはもとの線形空間と”鏡合わせ”のようになっている線形空間のことを指しています.
(実)線形空間の双対空間
とは,
から実数
への矢印(線形写像)を集めたものです. ここでまた関手を作っていきましょう.
の行き先は
です. アスタリスクが上付きになっていることから察せるかもしれませんが, 矢印の向きが逆になります.
を
から
への矢印として,
を作っていきます.
を
の元, すなわち
から
への矢印とします. さっきと同じように
が
から
への矢印になるようにしたいのですが,
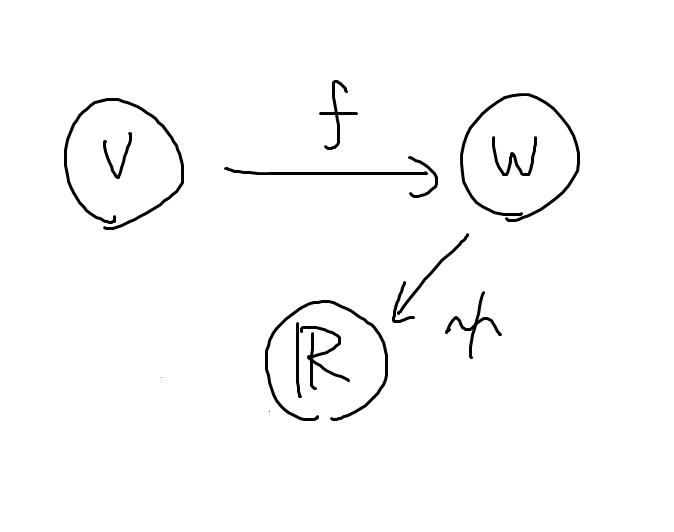
もう簡単ですね.
これで無事から
の矢印を作ることができました. 式にすると
です. こういう矢印の向きを逆にする関手を反変関手と言います.
微分形式
それでは微分形式を定義していきますが, 実は微分形式には次数というものがあって, それが2以上だとテンソル積とか外積代数とか難しいあれこれが必要になってきます. なのであんまり立ち入らずに雑に性質だけ述べていきたいと思います. 要するに嘘をつく宣言です.
次微分形式を定義する前に,
コベクトルというのを定義します.
の
コベクトルとは, ベクトル(
の元のこと)を
個受け取って, 実数を返すもののことをいいます(本当はもうちょっと条件がある). 図にするとこうです.

さっき解説した双対空間は, 1コベクトルを集めたものと言えます.
これで準備が終わったので本題に入ります. 次微分形式とは,
の各点
ごとに
の
コベクトルを対応させたもののことです.
と書いたりします. また, 各点に接空間の元を対応させたものをベクトル場といいます. こっちは名前でイメージしやすいですね.
微分形式の引き戻し
接ベクトルは”押し出す”ことができましたが, 微分形式は”引き戻す”ことができます.
多様体と
があって,
から
への矢印
があるとしましょう. このとき
の
次微分形式
を引き戻して
の
次微分形式
が作れます.
の各点
ごとに
の
コベクトルを見つけてくればいいので,
個のベクトル
を用意しておきます. あと, 簡単のために
としておきましょう.
さて, は
上の
次微分形式だったので,
の
コベクトル
があります. そして,
は
によって
に送ることができました. よって
にベクトル
を与えることで, ”自然”に実数を得ることができます. 式にすると
こうなります.
1次微分形式の場合に, さっきの双対で考えた反変関手を使ってやると,
となって, ベクトルを取らずともとできます. だから何だって話ですが…
おわりに
矢印を組み合わせるという”自然な”発想でいろんな関手が作れるということを見てきましたが, なんとなく自然さを感じ取っていただけたでしょうか. ホモロジーとかの話もしたかったんですけど, 僕がそこまで詳しくないのと分量の都合でなくなりました.
ではまた次の記事で.
おまけのネタがねぇ